
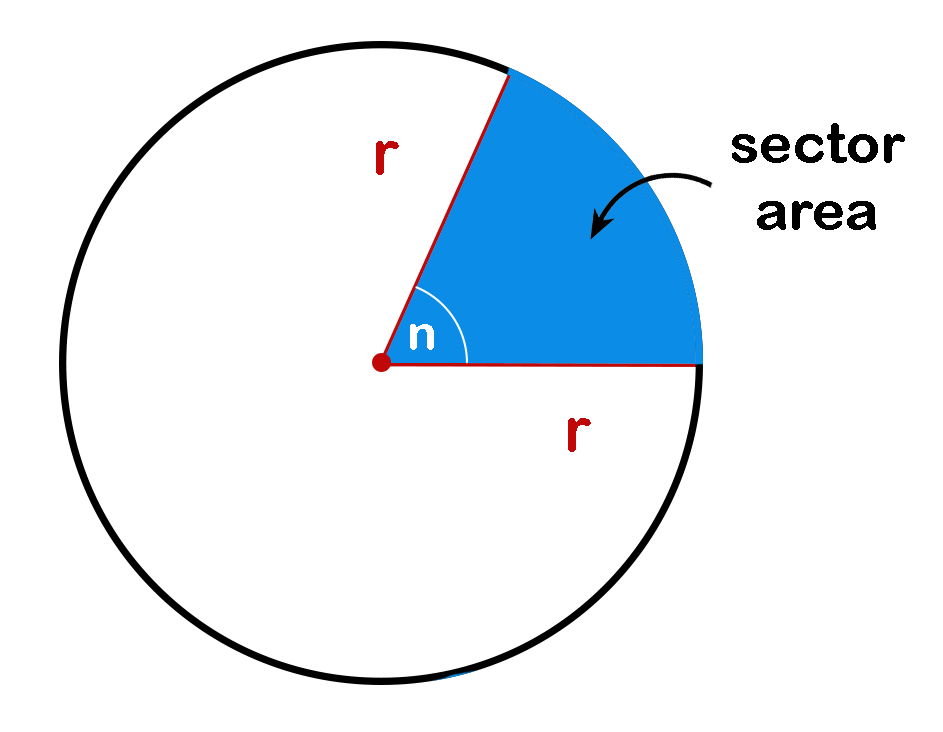
It’s also worth pointing out that as multiplication and division are both commutative, we could perform these operations in either order. So we can answer that if we’re given the circumference of a circle, we can multiply it by its radius and then divide by two in order to work out its area. If we then divide by two, this will cancel with the two in the numerator, leaving just 𝜋𝑟 squared which is our area formula. So this becomes two 𝜋𝑟 squared, which is looking a lot more like our area formula. If we first multiply by 𝑟, we’ll have two 𝜋𝑟 multiplied by 𝑟. Let’s start with our formula for the circumference of a circle, two 𝜋𝑟. But actually, we don’t need to go all the way back to finding the radius.

Circle's True Area ( /4) × D 2 ( /4) × 3 2 7.07 m 2 (to 2 decimals) The estimate of 7.2 m 2 is not far off 7. Estimate of Circle's Area 80 of Square's Area 80 of 9 7.2 m 2. So the question is if we know the circumference of a circle, what can we do with this value in order to work out its area? Well, we could work all the way back from knowing the circumference of a circle to find its radius and then substitute this value into the area formula. Example: Compare a square to a circle of width 3 m. As the area formula uses 𝑟, we’ll consider the circumference formula, which also uses the radius of the circle. The area can be found using the formula 𝜋𝑟 squared. The circumference of a circle can be found using the formula two 𝜋𝑟 or 𝜋𝑑, where 𝑟 represents the radius of a circle and 𝑑 represents its diameter. Let’s go ahead and write these formulas down. So in this question, we’re being asked to identify the link between the formulas we used to calculate the circumference and area of a circle. How can you use the circumference of a circle to work out its area?


 0 kommentar(er)
0 kommentar(er)
